絕對值是有理數(shù)學(xué)習(xí)的重點和難點，在考試中經(jīng)常會涉及到一些難度比較大的題目，經(jīng)常會與數(shù)軸結(jié)合考查，運用到數(shù)形結(jié)合思想和分類討論思想。為了更好地學(xué)習(xí)、理解和掌握絕對值，應(yīng)該從以下幾方面的知識點和題型如入手。

絕對值的概念是基礎(chǔ)和重點，必須要理解和掌握：

從定義上來看，絕對值表示的數(shù)軸上某個點與原點之間的距離，距離是一個非負數(shù)值，所以絕對值具有非負性，這是絕地值非常重要的一條性質(zhì)。

對于絕對值的意義不能去死記硬背，需要去理解，在絕對值的理解上，可以從兩方面去理解：

絕對值的幾何意義其實就是絕對值的定義；絕對值的代數(shù)意義其就是絕對值的性質(zhì)，在有關(guān)絕對值的題目的解答中，必然會運用到絕對值的定義和意義。

在絕對值的學(xué)習(xí)中一般需要掌握以下常見的題型：

1.首先就是絕對值的定義和意義的理解，通常會以判斷題的形式出現(xiàn)，屬于概念的理解，比較容易犯錯，需要多去進行練習(xí)，不但要學(xué)會判斷正誤，還需要去闡明理由，在練習(xí)中加深對絕對值的理解。

例題：

2.求一個數(shù)的絕對值，比較基礎(chǔ)的題目，直接根據(jù)絕對值的代數(shù)意義進行計算既可：非負數(shù)（0和正數(shù)）的絕對值等于它本身，負數(shù)的絕對值等于它的相反數(shù)。

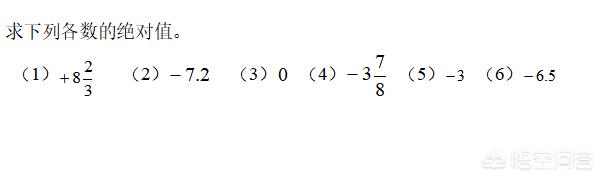
3.絕對值與有理數(shù)的運算，需要注意以下兩方面：

①、在運算中有絕對值時，一般需要先求絕對值，如果不能直接求出，需要根據(jù)絕對值的代數(shù)意義先化簡絕對值，再進行運算。

②要注意一個負數(shù)的絕對值的相反數(shù)和一個負數(shù)的相反數(shù)的區(qū)別，看起來有點相似，但區(qū)別很大，初學(xué)者比較容易混淆。

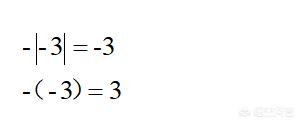
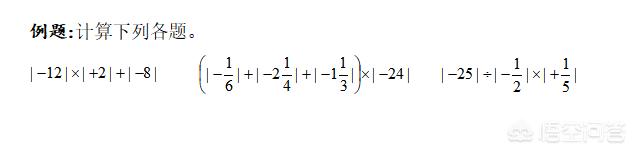
3.利用絕對值比較兩個負數(shù)的大小：

有理數(shù)的大小比較：

正數(shù)都大于0；

負數(shù)都小于0；

正數(shù)大于一切負數(shù)；

兩個負數(shù)，絕對值大的其值反而小．

比較兩個負數(shù)的大小，除了利用絕對值外，還可以在數(shù)軸上表示出需要比較大小的兩個數(shù)，再根據(jù)數(shù)軸上右邊的數(shù)總比左邊的數(shù)大，進行比較既可。

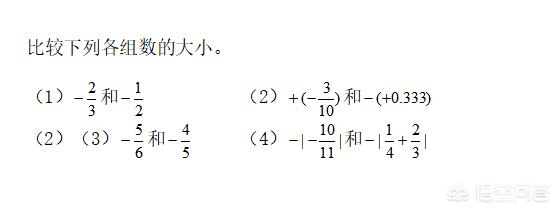
4.絕對值在有理數(shù)加法運算中的應(yīng)用

先來看看有理數(shù)加法運算的運算法則：

從運算法則中可以看出，在進行有理數(shù)的加法運算中，需要運用到絕對值的相關(guān)知識點。

5.絕對值的實際應(yīng)用應(yīng)用：

在某些實際問題的解答中，需要幾何絕對值的意義進行比較和計算：

如：

在上面這個問題中，需要比較各“起飛時間”的絕對值，絕對值越小越好。

如：

在第（4）小問的解答中，需要先計算出這天所走的總路程，那么就需要將上面的所有行程的絕對值相加，再進行計算。

5.絕對值的非負性的應(yīng)用：

任意數(shù)的絕對值都是一個非負數(shù)；

幾個非負式之和為0，則需滿足每個式子都為0。

有的題目中，根據(jù)絕對值的非負性，求一個含有絕對值的式子的最值。

5.利用絕對值的性質(zhì)進行化簡、求值：

這類設(shè)計的題型比較多：

①已知絕對值，求某個數(shù)：

②根據(jù)絕對值的求值。

③化簡：

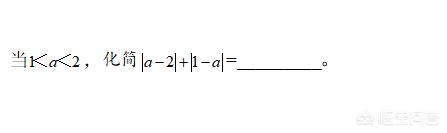
④化簡、求值

6.數(shù)軸與絕對值綜合：

根據(jù)點在數(shù)軸上的位置來進行大小比較、化簡和計算：

7.絕對值探究題：

一般需要根據(jù)絕對值的幾何意義去化簡、計算和判斷，通常需要結(jié)合數(shù)軸進行分析哈討論，體現(xiàn)出數(shù)形結(jié)合思想。

絕對值在學(xué)習(xí)和考試中常考的知識點及題型如以上所總結(jié)和歸納，需要在平時的學(xué)習(xí)中逐個去學(xué)習(xí)、攻克和突破，多加練習(xí)，掌握每種題型的特征及解題思路和方法。

本文鏈接：http://www.huatongxinda.com/wenzhang/34110.html

相鄰文章

• 上一篇：初一孩子成績班里倒數(shù)怎么辦 成績倒數(shù)第一怎么辦
• 下一篇：東海朱自清中學(xué)舉行2021慶國慶合唱比賽